Short Time Fourier Transform

• Why use STFT? We wants to know the frequency components at each time point.
• Solution: we perform FFT on small blocks. \(X(t,\omega) = \int_{-\infty}^{\infty}x(t^{\prime})w(t^{\prime} - t)e^{-j\omega t^{\prime} }dt^{\prime}\) where $w(t)$ is the window function.
• Window fuction will leak low frequency component to high frequency part. This leads to time-frequency uncertainty.

Time-frequency uncertainty

\(\sigma_t \times \sigma_{\omega} \leq \frac{1}{2}\) where $\sigma_t^2 = \frac{1}{E_t}\int t^2|w(t)|^2 dt$,$\sigma_{\omega}^2 = \frac{1}{E_{\omega}}\int \omega^2|w(\omega)|^2 d\omega$

• $\sigma_t \sigma_{\omega}$ can be used to evaluate the property of a window function.

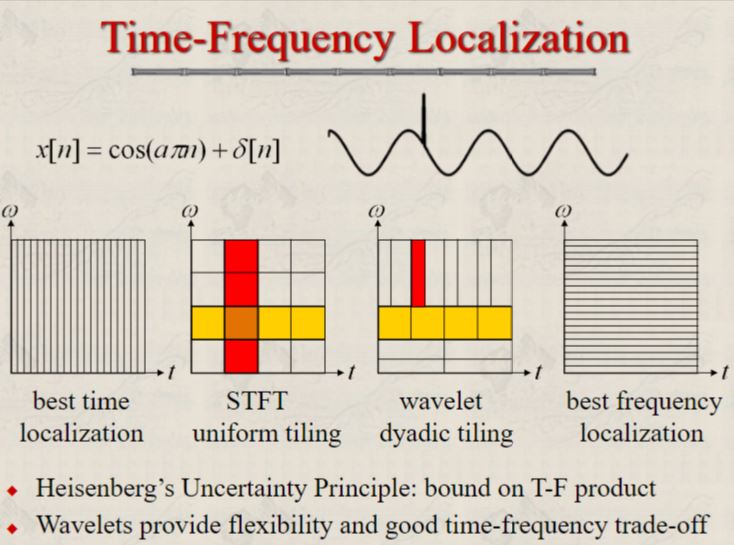
Time-frequency tiling

• The time and frequency resolution are the same over all time and frequency domain.
• However, for sharp transitions, we want to know extactly where that happpens. So, we need a high time resolution at high frequency.
• For smooth signals, we want to know the small changes on the signal (the texture). So, we need a high frequency resolution at low frequency.
• This leads to wavelet transform where different windows with different time/frequency resolution are used.

See this image: