Wavelet Transform

1 minute read

We know that wavelet transform comes from STFT by changing a single windowing function to a set of windowing functions. \(X(t,\omega) = \int_{-\infty}^{\infty}x(t^{\prime})w(t^{\prime} - t)e^{-j\omega t^{\prime} }dt^{\prime} = \int_{-\infty}^{\infty}x(t^{\prime})\phi_{t,\omega} (t^{\prime})dt^{\prime}\)
Rewrite the function \(\phi_{t,\omega}\) with two parameters: \(s\) scale and \(t\) time shift. We have the wavelet basis \(\phi_{t,s}(t^{\prime}) = \frac{1}{\sqrt{s}} \phi_m (\frac{t^{\prime} - t}{s})\) \(\phi_m\) is the mother wavelet. We can see that this is effectively changing the basis of the transform. Instead of transforming the signal into cosine basis, we find a different sets of basis functions.
It is used in compression (JPEG2000) and denoising, etc.

Representation of sharp changes: Fourier transform needs lots of cosines to represent a sharp changes, and it is affected by Gibbs effect. It is hard to get a sparse representation when there are edges in the signal.
Computational complexity: FFT – \(O(n\log(n))\), fast wavelet – \(O(n)\)
Both are orthogonal basis.
We can see this as multiple basis functions with non-zeros values at a small range, while FFT’s basis functions have values for the whole domain.

Low pass filters are averaging filters that approximate the signal and high pass filter produces details.
Thresholding can denoise the signal and there are multiple ways to choose the threshold.
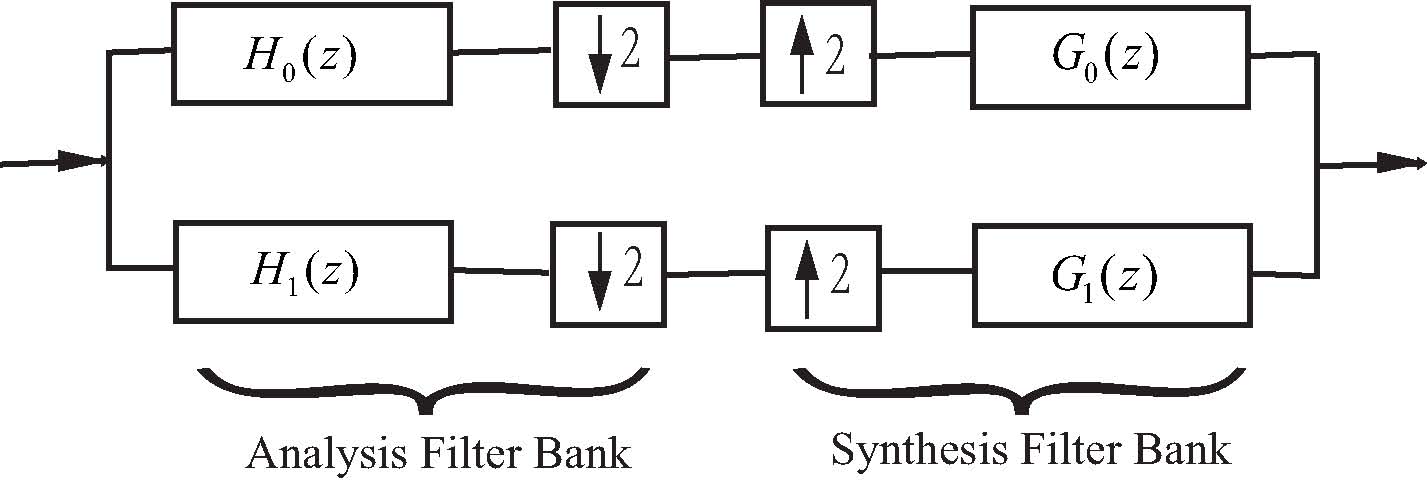
Because of the filtering, downsampling will not overlap the frequency bands.
When the length of the filter is larger than 2, boundary problems occur. (There are no boundary problems with the Haar wavelet!) There are two main ways to handle the boundaries: symmetric and period.(From Wavelet for kids.)