Nelder-Mead method/Downhill simplex method

• This method is a traditional method for non-linear optimization problem.
• A simplex is a structure in n-dimensional space formed by n+1 points that are not in the same plane.
• Requires no gradient calculation.
• Is traditionally used in dipole fitting model.
• Bad convergence property: cannot guaratee to coverge when dimension > 1. And it is getting worse when the dimension increases.

Methods:

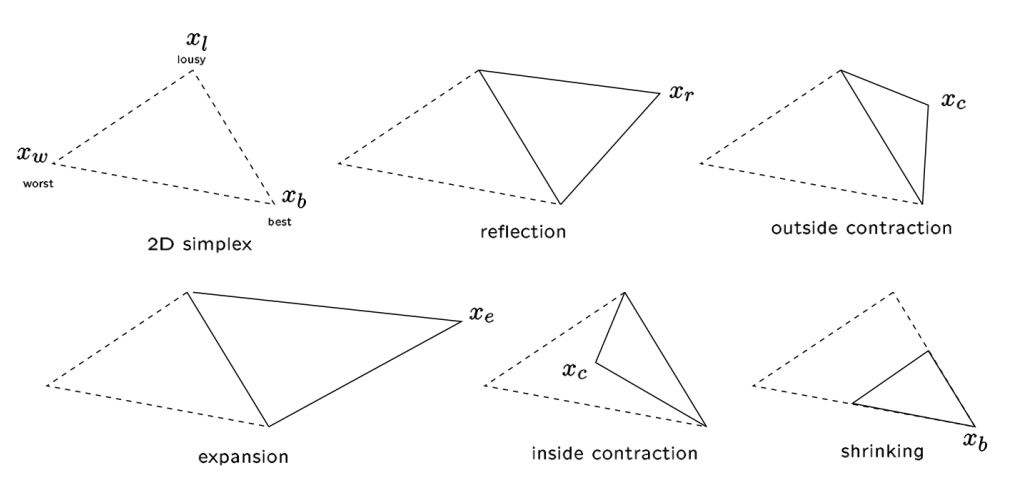
Basic idea: move the simplex by reflections, expansions or contractions

1. Sort. Evaluate \(f\) at the vertices and sort the vertices such that \(f_0 \leq f_1 \dots \leq f_n\)
2. Reflection. Compute \(v_r\), the reflectoion point of \(v_n\) and evaluate \(f_r = f(v_r)\). If \(f_0 \leq f_r < f_{n-1}\), replace \(v_n\) with \(v_r\).
3. Expansion. If \(f_r < f_0\),(means this is a good direction and we can go further), compute the expansion of \(v_r\), \(v_e\) and evaluate \(f_e = f(v_e)\). If \(f_e < f_r\), replace \(v_n\) with \(v_e\). Otherwise, replace \(v_n\) with \(v_r\).
4. Outside contraction. If \(f_{n-1} \leq f_r < f_n\), compute the outside contraction point \(v_{oc}\) and evaluate \(f_{oc} = f(v_{oc})\). If \(f_{oc} < f_r\), replace \(v_n\) with \(v_{oc}\). Otherwise, go to step 6.
5. Inside contraction. If \(f_r \geq < f_n\), compute the inside contraction point \(v_{ic}\) and evaluate \(f_{ic} = f(v_{ic})\). If \(f_{ic} < f_n\), replace \(v_n\) with \(v_{ic}\). Otherwise, go to step 6.
6. Shrinkage. For \(1 \leq i \leq n\), define \(v_i = v_o + \delta (v_i - v_o)\)